What you read in this article:
Harmony Search :
I , Arslan Mirbzergi,in this article I will familiarize you with the search for harmony completely. Search harmony is one of the best ways to optimize one-goal problems. The reason for naming this type of search is because in this algorithm, each decision variable acts like a musician and each value acts like a note. The algorithm was developed in 2001. The main purpose of this algorithm is routing in wireless sensor networks in order to extend the life of these networks.

What is harmony search?
In the introduction section, we said that search harmony is one of the best ways to optimize one-goal problems and its main goal is to routing wireless sensor networks in order to extend the life of these networks. This algorithm has a simple concept because it is useful and useful for problems related to continuous and discrete optimization and also the amount of mathematical calculations in it, has a simple concept and fewer parameters as well as easier implementation is one of the most widely used algorithms related to optimization.
If we want to make a comparison between search harmony and other meta-heuristic algorithms, harmony search has fewer mathematical calculations and this algorithm can be used by changing parameters and operators in different engineering problems. Another advantage of harmony search compared to genetic method is that in harmony search method, unlike genetic method, all solutions in memory are used.Having this feature has increased the flexibility of the algorithm in search of better solutions. In addition, another feature of Harmony Search is that this search identifies suitable solving spaces in less time. Of course, this feature, if our problem has local or Optimum Local, makes harmony search algorithm difficult and does not allow it to reach global optimum. This is one of the failures of the harmony search algorithm.
Steps of harmony search algorithm
The steps of harmony search algorithm are as follows:
- Rae initial responses along with their evaluation and filling HM memory
- Production of a new harmony with the possibility of using HM Equal to HMCR
- Change the frequency with par or pitch rate adjustment probability as well as evaluate new responses
- Compare new harmony with the previous one and add it to HM if it is optimal
- Go back to step 2, if there is no stop bet.
With the probability of PAR, we make small changes in the component we want.
How harmony search algorithm works based on descriptions related to part 4:
Parameters of harmony search algorithm
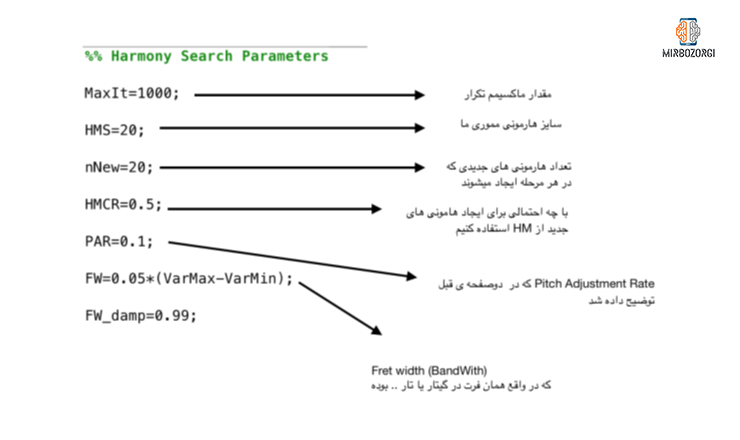
Harmony search algorithm is composed of a number of parameters that we will explain separately about each one.
- Maxlt: This parameter represents the values associated with the repetition of the algorithm.
- HMS: HMS or harmony memory size is a parameter that represents the amount of harmonies that are stored in memory.
- nNew: This parameter represents the amount of new harmonies that are made each time.
- HMCR: HMCR or harmony Memory Consider Rate is a parameter that shows the probability of using memory harmony. For example, if we put it at 0.5, it means that when creating a new harmony, there is a 50% chance that memory harmony will be used. This feature is almost identical to the selection feature in the genetic algorithm.
- PAR : PAR or Pitch Adjustment Rate is a parameter that shows the probability of minor changes in a component. This feature is almost identical to the mutation feature in the genetic algorithm.
- FW: FW or Fret Width is a parameter used for continuous problems. The name of this parameter is derived from fret or guitar or violin. The value of this parameter should be proportional to the distance between VarMax and VarMin, so we can say that the value of 0.05* (VarMax-VarMin) is almost significant. Instruments such as piano, unlike instruments such as guitars, do not have firth.
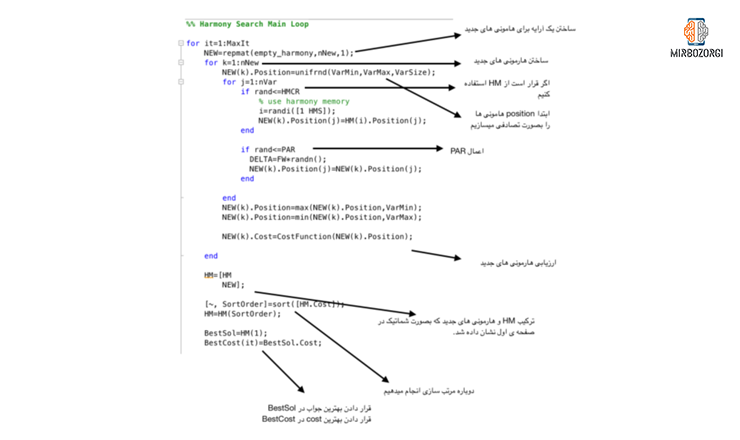
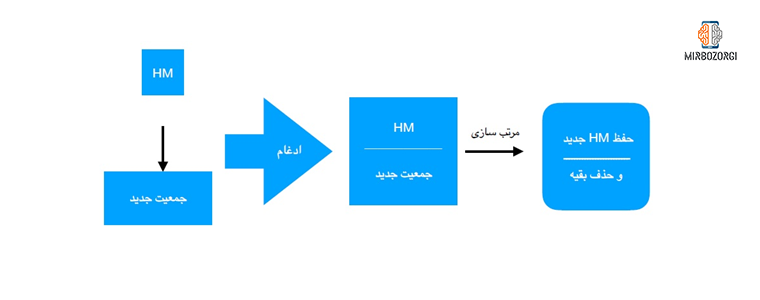
The general description of the steps of the harmony search algorithm is as follows:

A more detailed description of harmony search algorithm
In the photos above, the parts are numbered in red, which we will explain about each one in this section.
- This section includes the construction of a raw harmony and the acts of reproduction and …. On it. This harmony is able to store information about each response. Therefore, it is necessary to pour information into it further. This is a raw harmony of the main features of positon and cost, in which the cost corresponds to the position.
- This part is related to the proliferation of raw harmony 20 times. The reason for the repetition is that we put the HMS rate at 20.
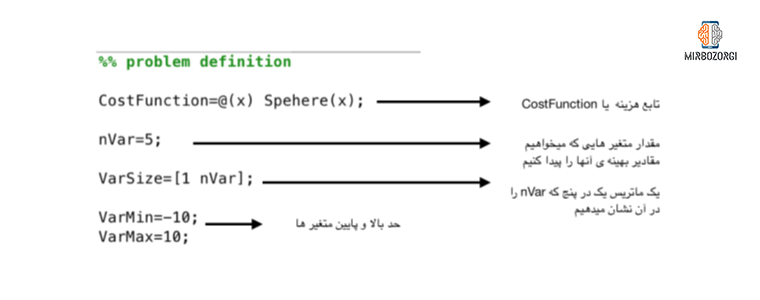
- Depending on the nVar value, each response contains 5 different elements. These 5 elements are in the form of a matrix of 1 in 5. The members of this matrix are between -10 and 10. (Between VarMax and VarMin values). At this point, the capacity of raw harmony must be filled by random information. As a result, it is formed by repetition. The amount of this repetition is determined by HMS values. If we randomly form a 1-in-5 matrix and the members of this matrix randomly contain VarMax and VarMin values, the created responses will also be random. In this case, we can create random solutions by using unifrnd (a function of statistical tools). After producing these random answers, we evaluate them for their position.
- This step relates to the sorting of memory harmonies. This sorting should be based on cost. After this step, the first phase of the harmony search algorithm is finished.
- At this point, we save the best solution in BestSol. We also keep the best amount of cost until all repetitions are finished. In other words, until the end of the number of repetitions (MaxIt), each time, we store the best answer in BestSol.
- This step consists of a loop that is actually the main loop of the program and repeats as much as mentioned in the MaxIt parameter. In this case, we need to create an array for new harmonies. The above array has the capacity to hold new harmonies at the rate of nNew.
- Each time you repeat the ring of the previous step, we fill the position of a harmony randomly.
- The loop in this section is repeated as much as nVar. In each of these iterations, if the random value is equal to HCMR or smaller than that, a member of HM is randomly selected and the position of jM member of iM HM is placed in the jM position of the k member of the new array. If the random value is greater than HCMR, the answer is made randomly. In another condition, if the random value is equal to PAR or smaller than that, the answer is made randomly using FW values and applied to the jM position of the kth member of the new array.
- This section relates to the application of restrictions. If a position is withdrawn from VarMin or VarMax, we will return it to VarMin or VarMax.
- This step involves evaluating the answers from start to finish and sorting them and forming BestCost andBestSol.
Test on sphere function
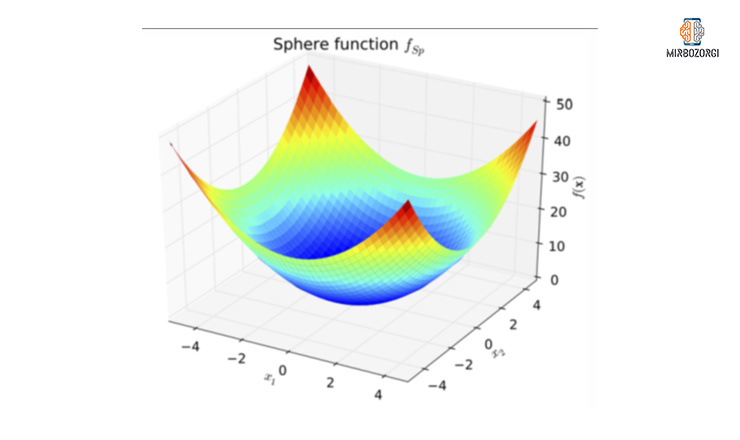
The lowest value of this function in the range [-10,10 ] and for the Sphere function is equal to 0, which the harmony search algorithm is reasonably close to, as:
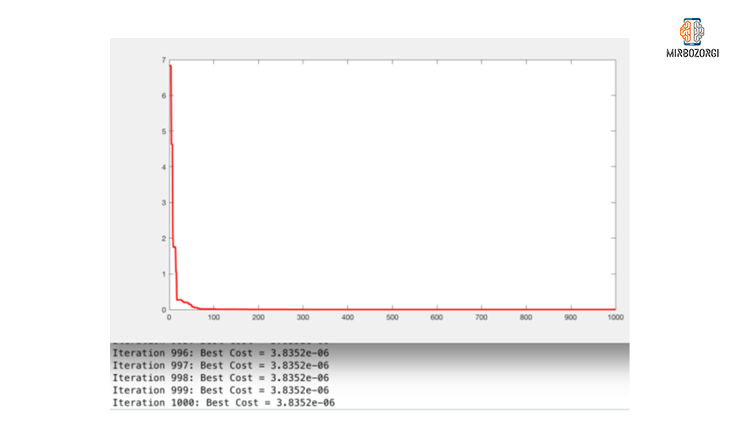
As you can see, after 17 repetitions, the best cost value has reached below 1. Finally, in the 1000th iteration, it reached 06e-3.8352, which is very close to 0.
Test on DeJongs function
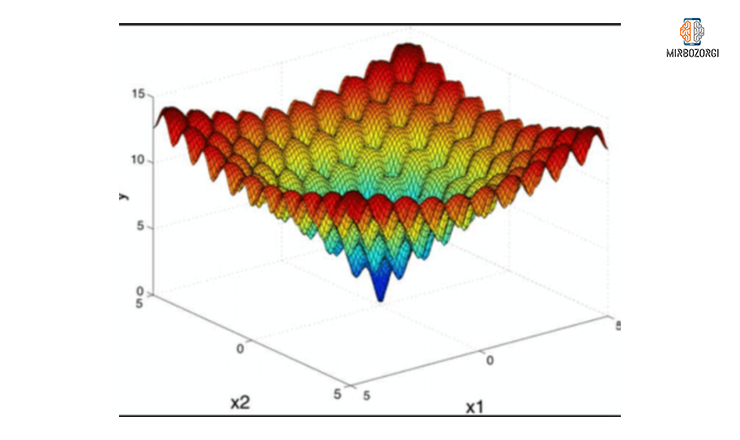
From the function diagram, you can see that this function has many local optimal solutions. As a result, harmony search algorithm should have a good scanning capability so that optimal local solutions are not generated for it. For this purpose, we use PAR and HMCR parameters.
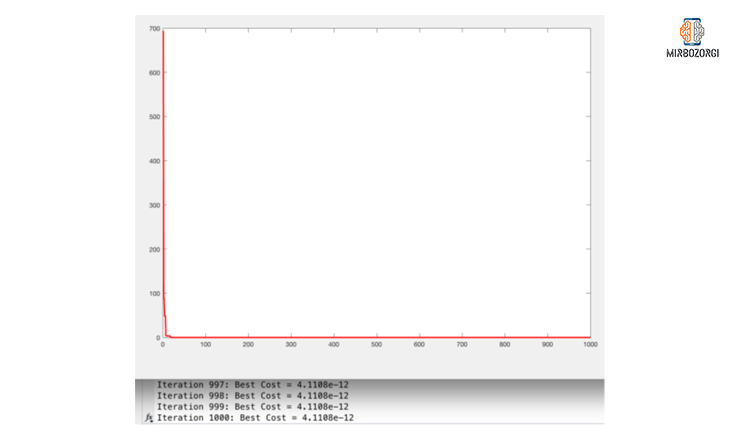
As you can see in the function chart, in the range of -10 to 10, the lowest of this function is 0. In the first iteration, the value of this function is 694.0663 and in 18 iterations its value has reached to 0.23157 and in the 1000th iteration this number has reached 12 e-4.1108, which is very close to zero.
Test on Griewank function
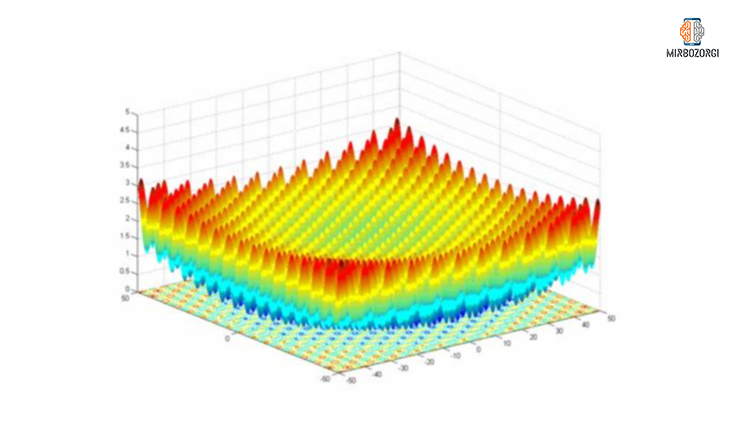
There are many optimal local solutions in the Griewank function. As a result, harmony search algorithm should have a good scanning capability to produce acceptable global optimal solutions for it.
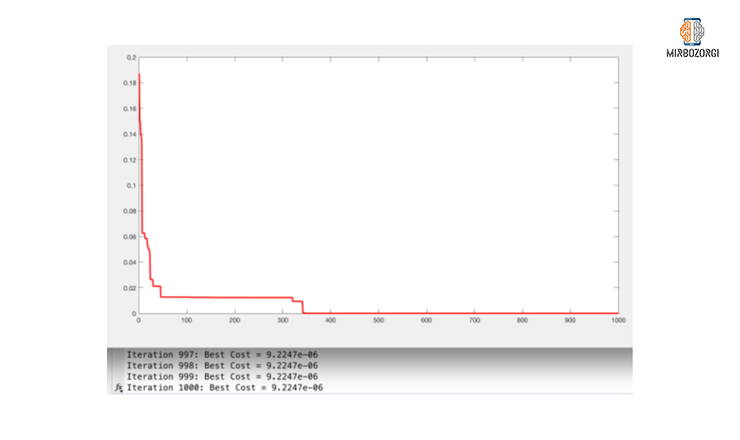
As you can see in the function chart, in the range of -10 to 10, the lowest of this function is 0. In the 1000th iteration of this function, the bestcost value has reached 06 e-9.2247, which is very close to zero.
Test on Rosenbrock function
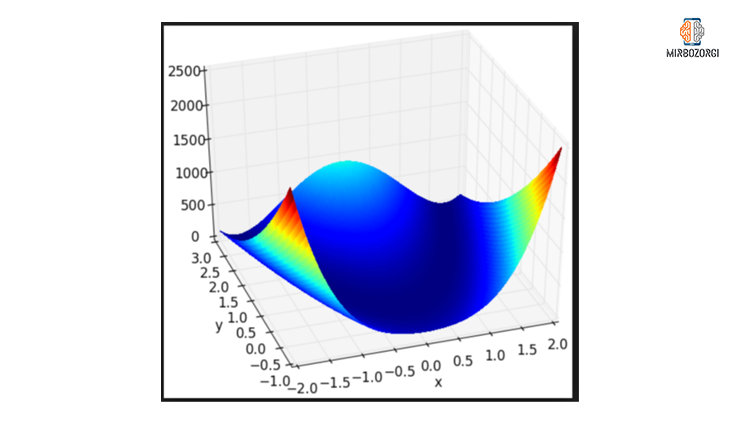
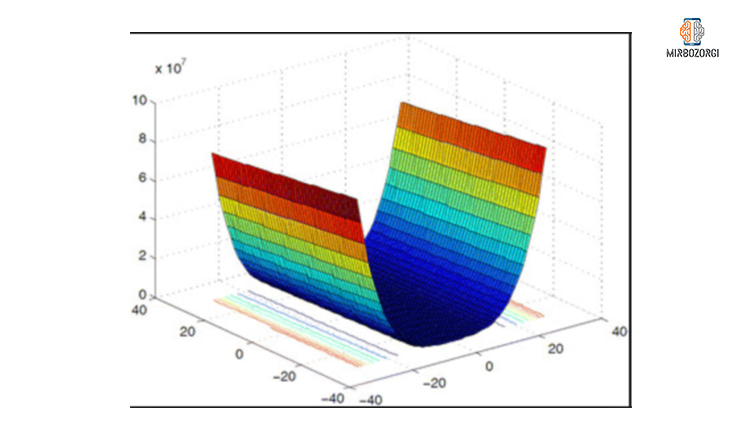
As you can see in this chart, the lowest value of this function, in the range of -10 and 10, is approximately zero.
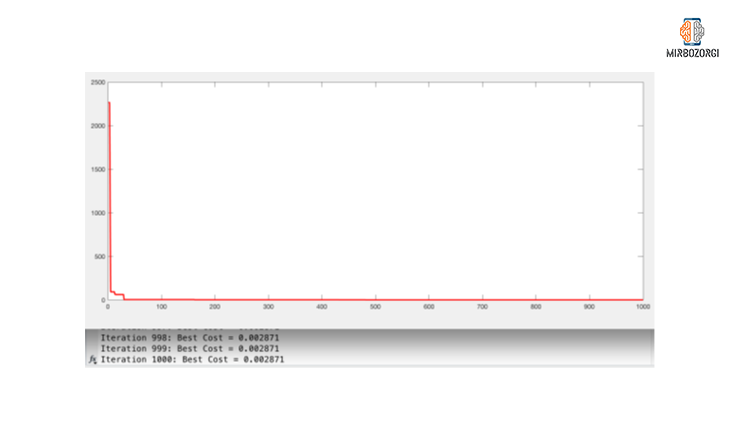
As you can see in the function chart, in the range of -10 to 10, the lowest of this function is 0. In the first repetition, the value of this function was 2263.9681 and in 432 repetitions its value reached below 1. Also, in the 1000th iteration of this number has reached 0.002871, which is very close to zero, and with more repetition, the bestcost value will be closer to zero.
The Rastrigin function does not work on the harmony search algorithm. Also, this function on the PSO algorithm lacks the appropriate answer. (The appropriate answer was zero, which in both algorithms, this function was far from that. )
And in the end,
Mirbazorgi’s website aims to help you learn and fix your problems by providing articles andpractical experiences. Email me if you have any questions.